Mathlets
kirky
2019-02-14T23:28:38-05:00
Here you will find a suite of dynamic Javascript “Mathlets” in Kreyòl, for use in learning about differential equations and other mathematical subjects, along with examples of how to use them in homework, group work, or lecture demonstration, and some of the underlying theory. There are also voice-over animated demos.
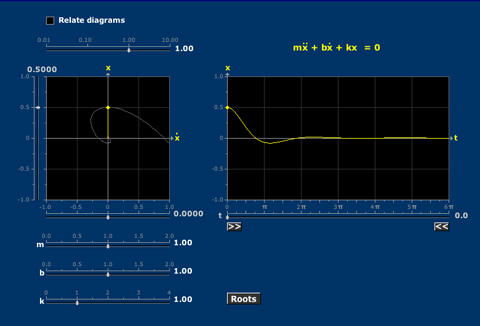
Damped Vibrations
The decay from initial condition to equilibrium of an unforced second order system can be understood using the roots of the characteristic polynomial and the phase diagram.
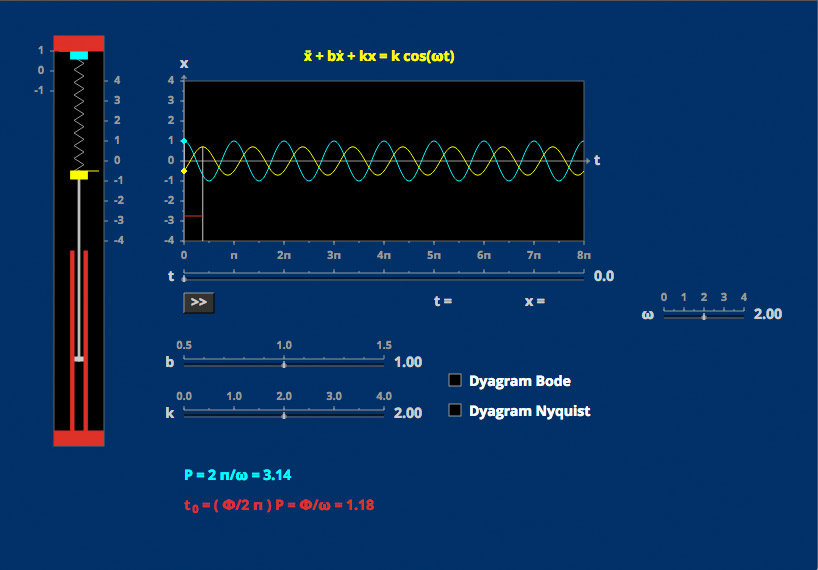
Amplitude and Phase Second Order I
A spring drives sinusoidally a spring/dashpot/mass system. The predictable amplitude and phase lag of the sinusoidal system response can be understood using Bode and Nyquist plots.
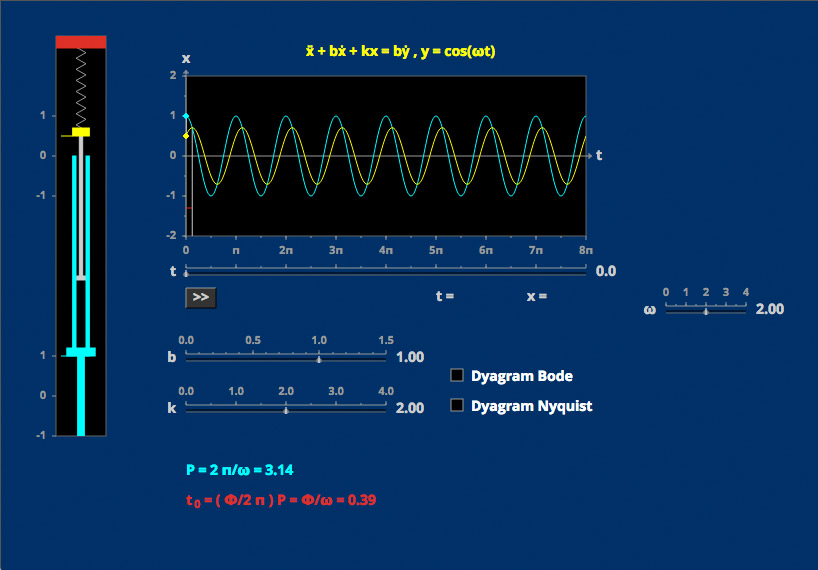
Amplitude and Phase Second Order II
A dashpot drives sinusoidally a spring/dashpot/mass system. The predictable amplitude and phase lag of the sinusoidal system response can be understood using Bode and Nyquist plots.
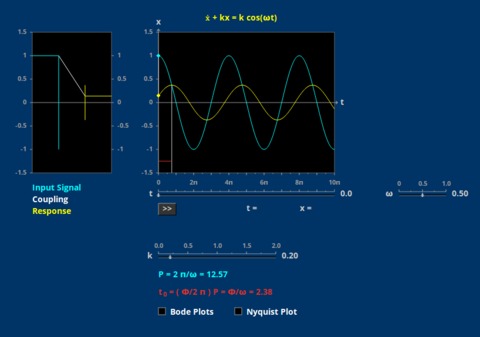
Amplitude and Phase First Order
The tide in a harbor lags behind that of the open ocean, and is controlled by a first order linear equation. Bode and Nyquist plots illustrate the steady state and method of solution.
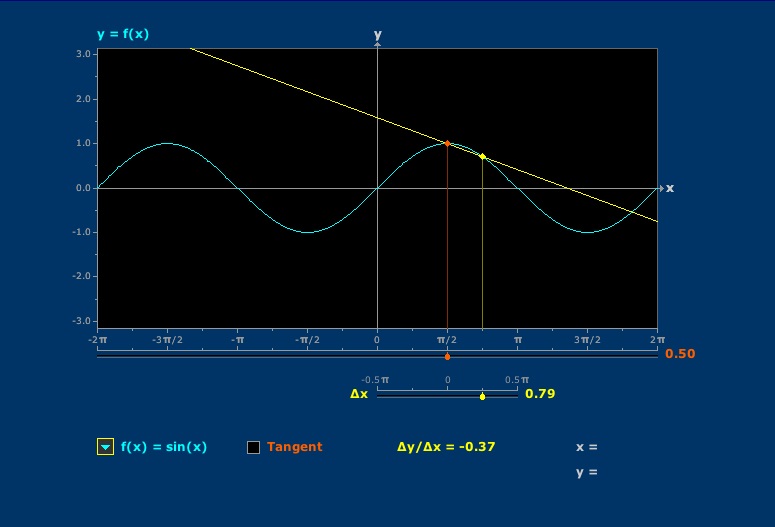
Secant Approximation
Secants converge to tangent lines.
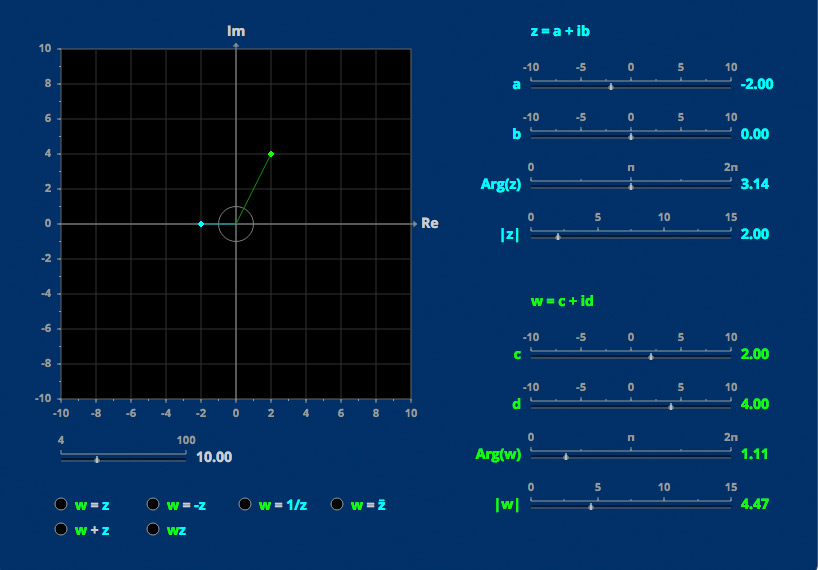
Complex Arithmetic
Complex numbers and operations on them can be visualized on the complex plane.
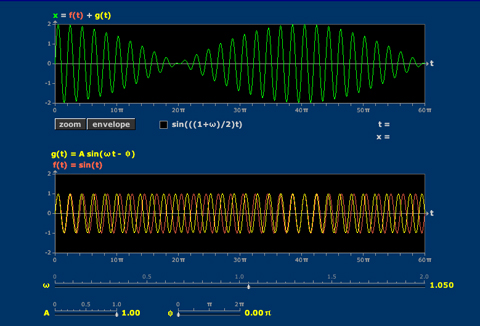
Beats
Beats occur when two sinusoids superimpose. The beat frequency is captured by an envelope.

Vector Fields
Nonlinear autonomous systems can have complicated solutions, which can be represented with some loss of information by their trajectories. Usually they behave nearly linearly near equlibria.
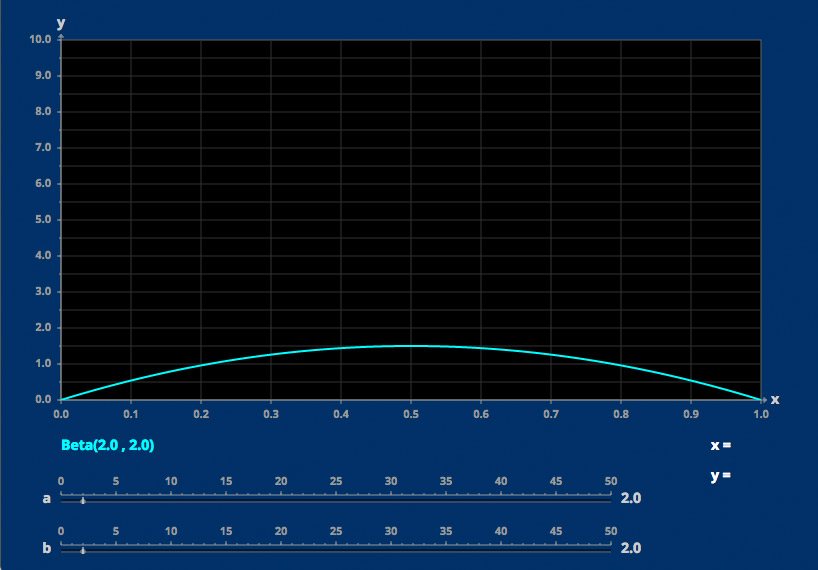
Beta Distributions
The beta-distribution depends on two parameters.
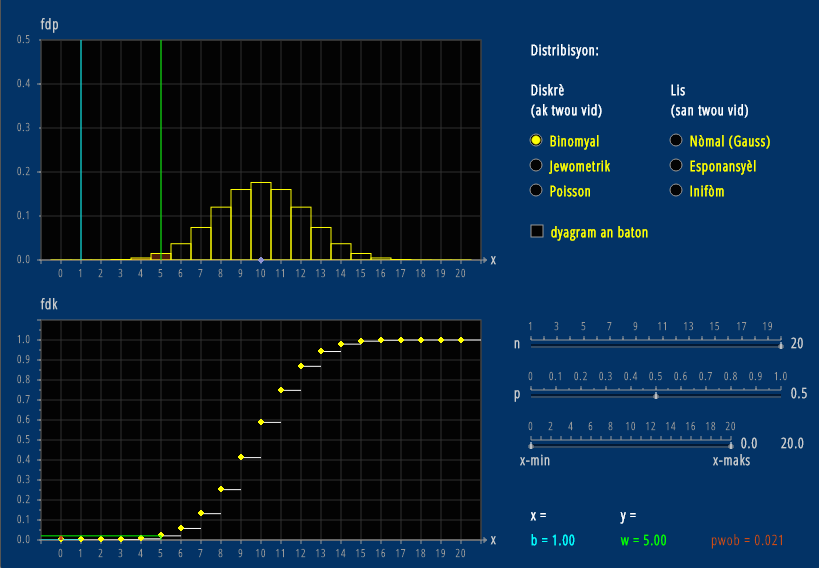
Probability Distribution
Different probability distributions are useful in different situations.
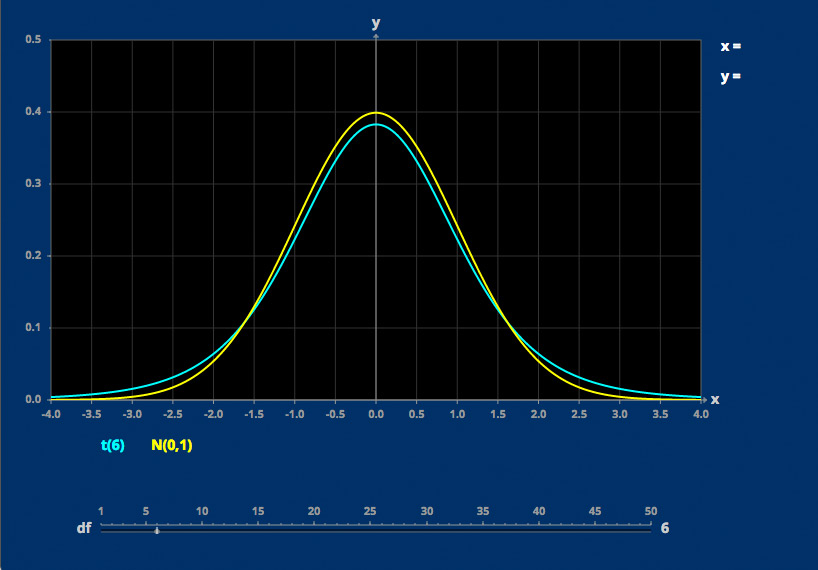
T Distributions
The t distribution depends on one parameter.
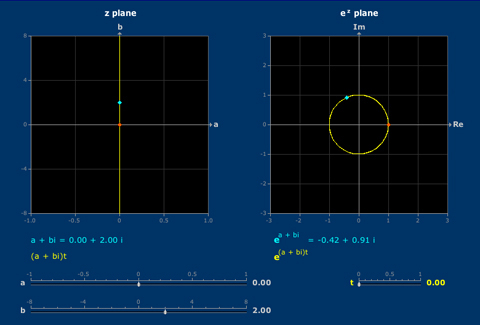
Complex Exponential
The complex exponential function sends straight lines through the origin to spirals.
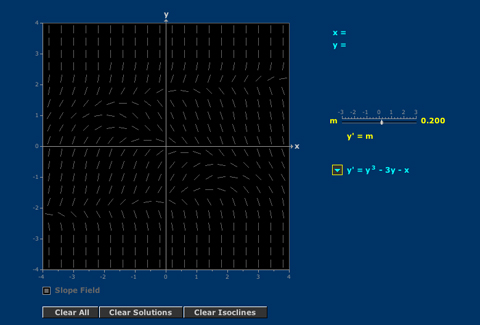
Isoclines
Graphs of solutions of a first order equation can be understood in terms of the slope field and isoclines.
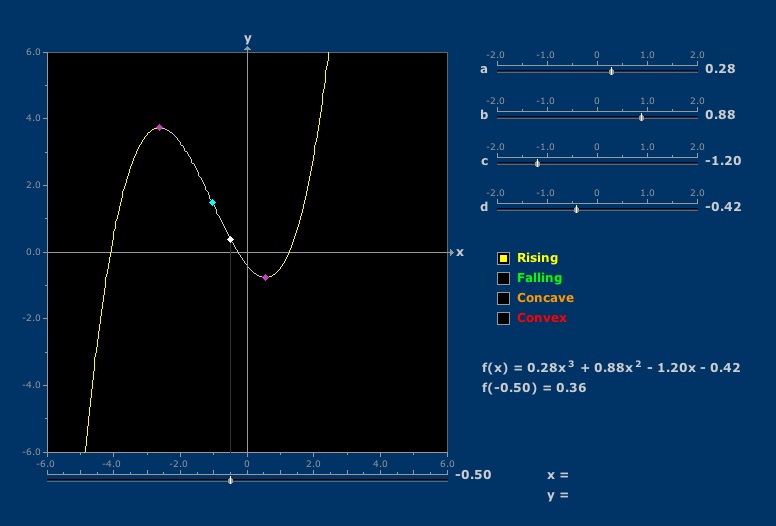
Graph Features
Portions of graphs of cubic polynomials rise, fall, or are convex or concave.
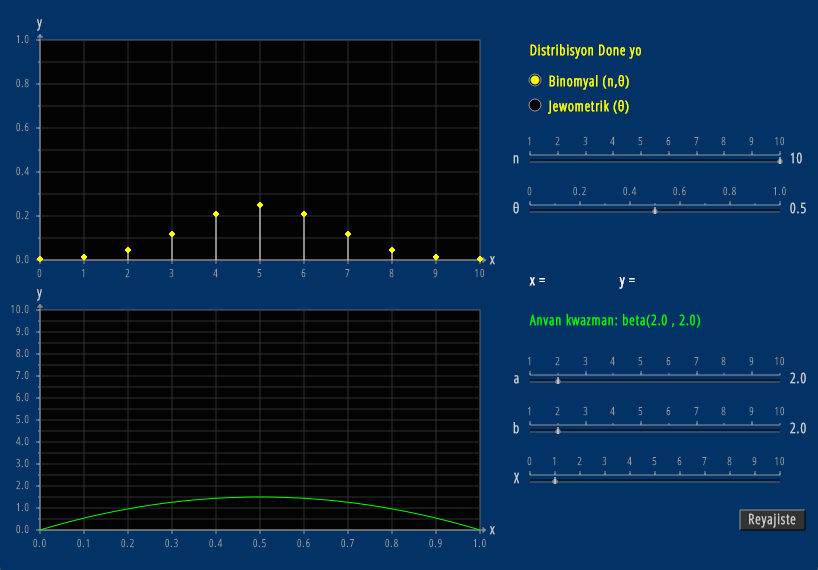
Conjugate Priors
Bayesian updating is easy with conjugate priors.
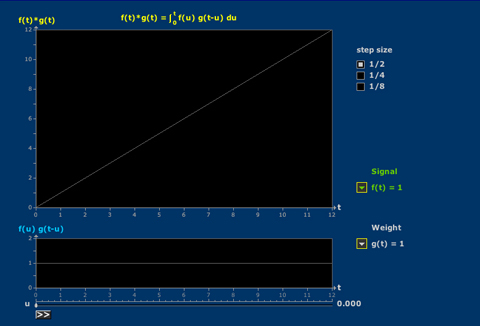
Convolution Accumulation
The convolution integral is the superposition of unit impulse responses.
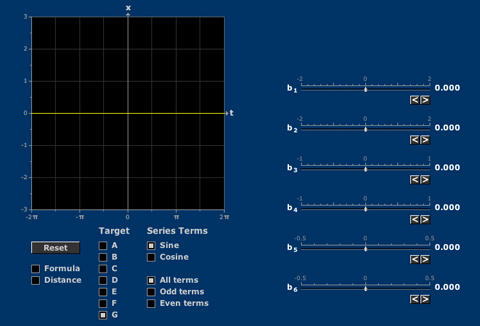
Fourier Coefficients
The initial terms of a Fourier series give the root mean square best fit. Symmetry properties of the target function determine which Fourier modes are needed.
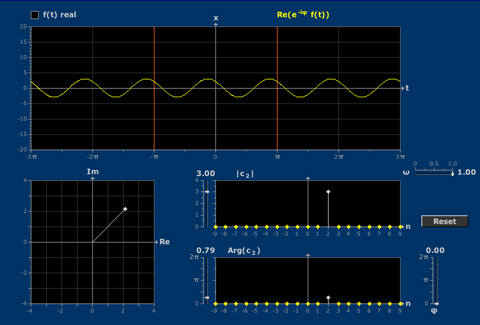
Fourier Coefficients Complex with Sound
The coefficients in a Fourier series, when it is viewed as a sum of complex exponentials, are best thought of in terms of their magnitude and argument. You can only hear the magnitudes, even though the arguments greatly influence the waveform.
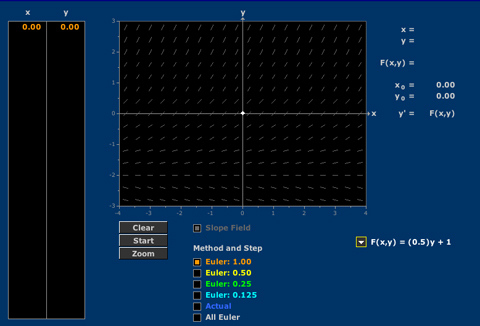
Euler’s Method
Given an initial condition and step size, an Euler polygon approximates the solution to a first order differential equation.
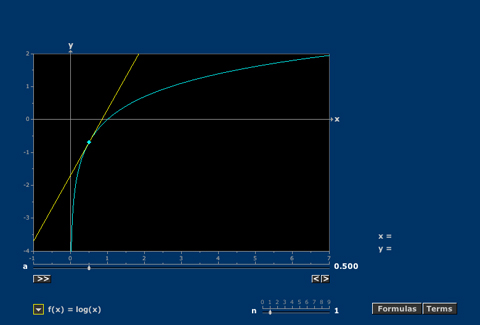
Taylor Polynomials
Most functions are well approximated near any point by a sequence of polynomials.
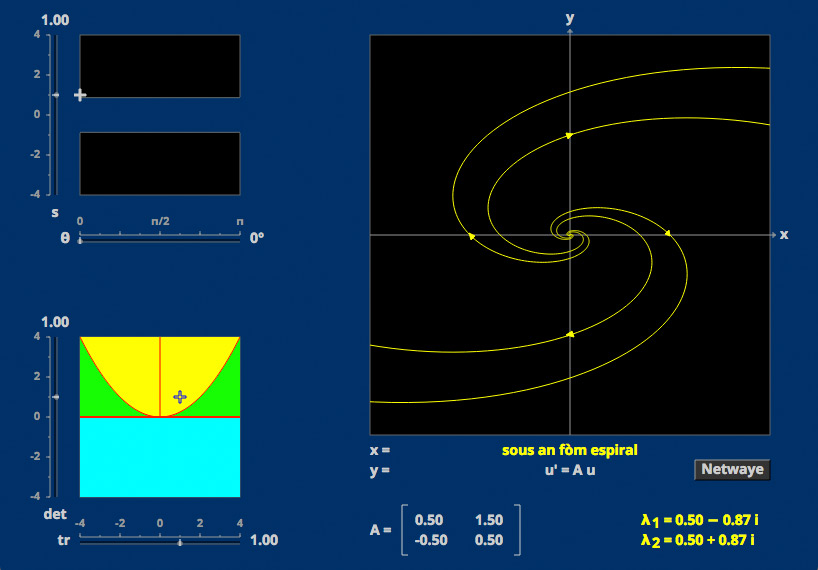
Linear Phase Portraits: Cursor Entry
The phase portrait of a homogeneous linear autonomous system depends mainly upon the trace and determinant of the matrix, but there are two further degrees of freedom.
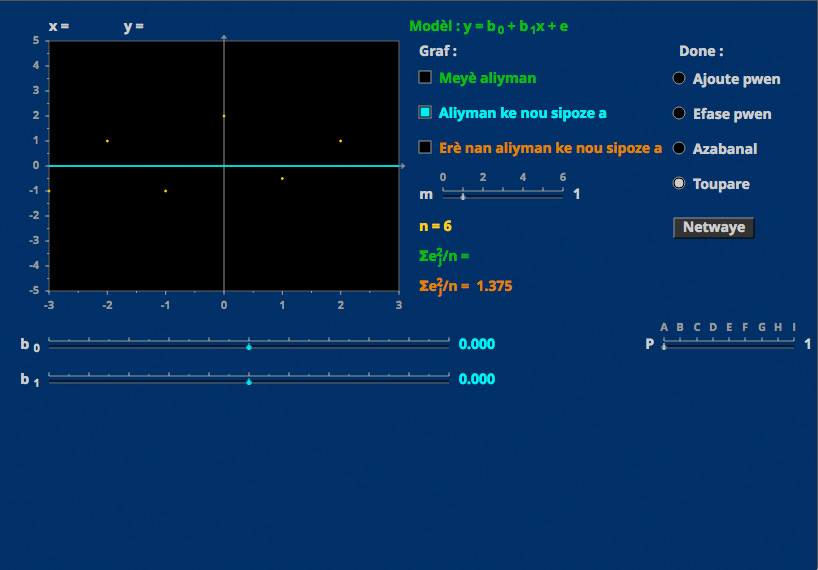
Linear Regression
Data can be fit by a class of functions using least squares.
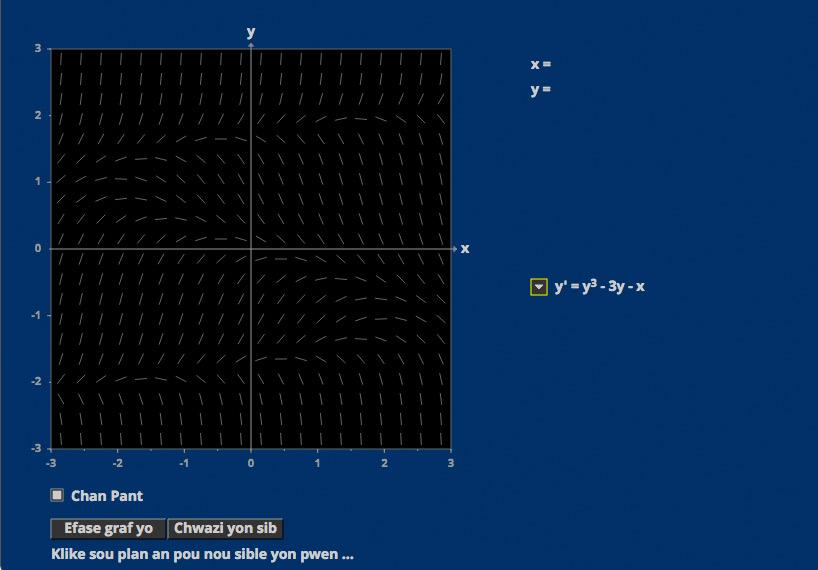
Solution Targets
Sometimes solutions converge as time increases, and sometimes they diverge, making the Uniqueness Theorem surprising.
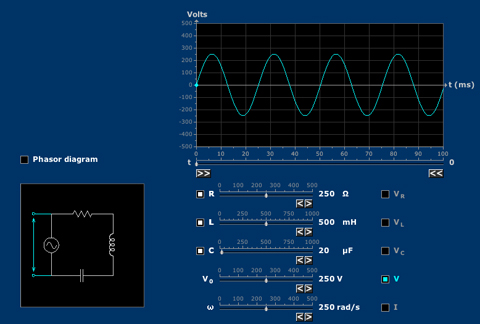
Series RLC Circuit
System responses of a sinusoidally driven RLC circuit can be understood by means of phasors.

Riemann Sums
An integral can be approximated as a sum in many ways.

Creating the Derivative
An integral can be approximated as a sum in many ways.

Ballistic Trajectory
A thrown stone responds to the forces of gravity and drag.
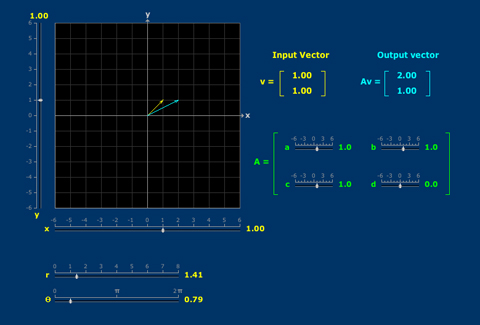
Matrix Vector
The product of a matrix and a vector depends in interesting ways on the entries of each. Eigenvectors represent a coincidence of direction.
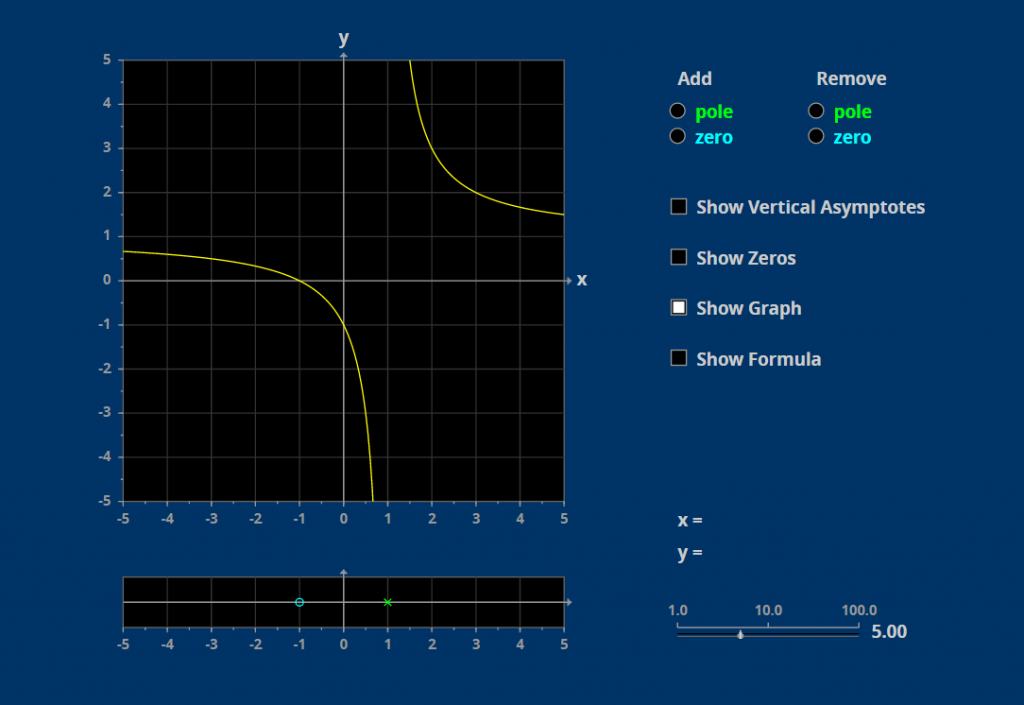
Rational Functions
The poles and zeros of a rational function let you make a rough sketch of its graph.
MIT Mathlets were initially developed under a generous grant from the d’Arbeloff Fund for Excellence in Education. Subsequent support came from the MIT Office of Digital Learning. Mathlets in Kreyòl are made possible by the same NSF grant that funds this MIT-Haiti Initiative.






























